Triathlon: should I deflate my tires in the sunny bikepark?

So what’s the ritual all about?

Competitors deflate their tires to prevent a possibly explosion, due to high pressure building up, itself due to the air getting really hot in the inner tube, thus reaching a pressure exceeding the resistance of the clincher or the tube.

The physical law behind

Fundamentally, it all starts from a perfectily founded observation.  Indeed, the black rubber of the clinchers or the tubes get energy from the sun, thus heat up the air inside, which wants to expand, due to dilatation, a natural physical phenomenon that nothing can prevent.  Since the air inside has a limited volume to take up (the inner tube’s); it can’t expand freely, so instead its pressure increases, much like inside a pressure cooker.  Except the resistance of the tire has a limit that is much lower than a pressure cooker, and may blow up past a critical pressure.
What sounds like a wise precaution first, may be an overreaction from the actual risk in presence.

So, could the tires possibly blow up?

What final pressure are we really looking at in practice?

Let’s go back to the fundamentals of static gases (as in, not flowing, which is the case in a tire).  What have we got?

We most likely have air in the tubes, which is a blend of gases, mostly nitrogen and oxygen.  The physics of real gases being a bit complicated, and not worth it for this subject; therefore we will make the commonly accepted approximation that air is a perfect gas, hence use the perfect gases law, which puts in relation its pressure, volume occupied, and temperature, as stated by the equation on the left.

In this equation, P is the pressure of the gas in the tube, V its volume, equal to the inner tube’s, since it fills it with no escape; T is its temperature, expressed in Kelvins (see Reference #1 down this page), that we will consider to be consistent in the inner tube, for simplicity’s sake; n is quantity of moles of the gas, basically the quantity of gas, in a special unit we will explain below; finally R is a constant, called the constant of perfect gases, equal to 8.31 J/K, that is, Joules per Kelvin, we will detail this too at the end of the topic, in the References section, although we don’t really need to make n and R intervene in the calculations here.

Immediate results

Since we have an equality, we can divide each member by another equality, in particular, we can stack these equations, the one above will be at state 2, after a couple of hours of the sun beating down on the tire, and the one underneath will be at state 1, when the competitor has just finished inflated his tires.
We can eliminate n and R from the equation, since we find them both in the numerator and in the denominator.
Two, we can eliminate a further term: The Vs, since V₂ is practically equal to V₁, since the tube/clincher barely expands despite the inner tube getting tighter underneath.  This is a direct practical observation from the experiment, we won’t need to demonstrate this.

As a result of the above, we get the simple ratio equation here.

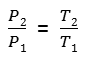
Myth 1 : T₂/T₁ is not that impressive

The first conclusion that this equation leads to, is that P₂/P₁ ratio varies exactly as T₂/T₁ does.  So, to have a meaningful growth of pressure in the inner tube, it would need T₂ much greater than T₁.  But, do we have this?
The bike has been hanging around the bikepark anyway.  It was not in a fridge or a refrigerating van just before, was it? So why, when the bike got inflated at 8 bars (116 psi), in the hotel room, or near the car that brought it to the bike check-in, would it have tires that were much cooler than after 2 hours of sun beating down on it in the bikepark?
We can accept, that in the worst case scenario, air was inflated to 8 bars (116 psi) or so, in a 21°C (70 °F) air-conditioned room at the hotel, then the bike got brought to a bike park that is seriously heated up by a strong summer sun, and there air may get to 50°C (122 °F), due to tar reflection.

So, what is the T₂/T₁ ratio worth in this worst case scenario?
Let’s see:
All temperatures must be handled in Kelvins (see Reference #1 down this page)

T₂/T₁ = (273.15+50) / (273.15+21) = 1.10 = 10%

Conclusion: despite the greate apparent temperature difference for the human, T₂ is only 10% greater than T₁ for physics.  Not really impressive.

Myth 2 : P₂/P₁ is not much more impressive

Given the formula we’ve shown earlier, P2/P1 equals T2/T1, meaning P2 is only 10% than P1 too.  Not exactly impressive.
In the example where P1=8 bar (116 psi), we’d have P2=8.8 bar (128 psi); whoa, do you think your tire will create a nuclear blast at 128 psi instead of 116?

Other natural occurrence of a 10% increase in pressure

To demonstrate that a 10% increase in tire pressure will not exactly burst your tire, I will now calculate what altitude creates the same stress on the wall of the tire.  It comes down to calculating at what altitude there is 10% less pressure on the outside wall of the tire, therefore creating a pressure difference ratio of 10%, that applies on every surface piece of the tire.  Next, do you think your tires may blow up as you pass that altitude and higher? Have you ever seen that on TV in July during Tour de France? Let’s answer these questions.

First, let’s consider the normal pressure condition of 1013 hPa (about 1 bar, or 1 kilogram per square centimeter) at sea level.
Let’s also consider an elementary surface of your tire, whatever surface, like a square centimeter for example;
now, the rubber faces a stress of a 1:8 ratio = 0.125
Why? Because we have 8 bar, or 116 psi, inside versus 1 bar or 14.5 psi, outside.

At what altitude will that ratio shift by 10%?
Well, if we assume the temperature stays the same as you climb up for a bit, the perfect gas law shows that there will still be 8 bar (116 psi) of pressure inside at different altitudes, but not outside, since the air is getting thinner.  There will be a 10% shift in the rubber stress when this ratio reaches 0.112, i.e an outside pressure of 912 hPa.
To find out the equivalent altitude, we need to know the relation between pressure and altitude.  It is a bit complicated to establish, and out of this topic, but Wikipedia supplies a good formula for it, that shows that the equivalent altitude would be around 900 m only!

That means that when you start to ride at sea level at the normal pressure of 1013 hPa, and you take your bike to only half of the height of Mt Ventoux summit, every square centimeter of your tire endures a 10% shift in pressure difference.  Do you think that cyclists experience a tire explosion as they go up Mt Ventoux and they pass 900 m ? (that’d be just a bit before the“yellow house”, wouldn’t it?)
Enough nonsenses! We have never seen this, nor this is supported by the laws of Physics, meaning there are no physical reasons why you should deflate your tires in the bikepark.

Legend / References

Kelvin

It’s the International System Temperature Unit.  Add 273.15 to Celsius degrees to get Kelvins.  For Farenheit degrees, convert to Celsius degrees and add 273.15 .  Under a normal pressure of 1036 hPa (see level), water freezes at 273.15 Kelvin.  Note that we don’t say“Kelvin degrees”, but just“Kelvin”, since this is a unit, not a scale.