A l’ombre de la Sainte-Baume
Puis Jean de Florette se termine, et vient l’automne, puis l’hiver. C’est alors que vous découvrez une autre lumière dans ce joli coin de Provence, à bicyclette, mais cette fois-ci sur le versant nord de la Sainte-Baume : sur le plan d’Aups. C’est la D95. Il est le milieu de matinée, et vous sentez que le soleil est juste-là, derrière la Sainte Baume. Pourtant une question vous taraude : est-qu’il poindra au dessus de la crête, à son point culminant, vers 12h30 ? Nous allons tenter d’apporter une réponse ci-dessous.

Avertissement
Cet article pédagogique s’adresse à un public capable de comprendre la notion d’ombre projetée, donc de la simple relation qui existe entre la hauteur d’un objet, la hauteur du soleil (= l’angle qu’il fait avec l’horizon), et la longueur de l’ombre. Cette relation s’appelle d’ailleurs la fonction tangente, en géométrie. Mais au pire, si vous ne comprenez pas ce qu’est tangente au juste, c’est pas bien grave, car de toute façon une simple calculatrice scientifique vous apporte la touche [tan], qui fait le calcul pour vous.
Notations utilisées
Les angles seront exprimés ou entendus en degrés, car on travaille en géographie, et non en radians comme c’est traditionnellement la cas en trigonométrie.
Rappel
- tangente : il s’agit du rapport entre la hauteur d’un triangle rectangle, ici verticale, et sa base, ici horizontale. Dans le cas qui nous intéresse, la tangente varie dans l’intervalle [0;, +∞]. En fait c’est tout simplement le rapport entre la hauteur d’un arbre et la longueur de son ombre au sol !
Activité cognitive
Le propos de ce sujet est de prédire l’existence aux limites d’événements favorables ou défavorables, dans un phénomène cyclique, lorsque l’on connaît la situation à un moment donné du cycle. Le cas du cycliste sur le D95 est un simple exemple. Mais le même principe s’applique pour savoir si une maison, une culture, ou des panneaux solaires, recevront du soleil toute l’année ou pas, et sinon, dans quelle fenêtre temporelle le soleil sera-t-il occulté.
Présentation de l’environnement
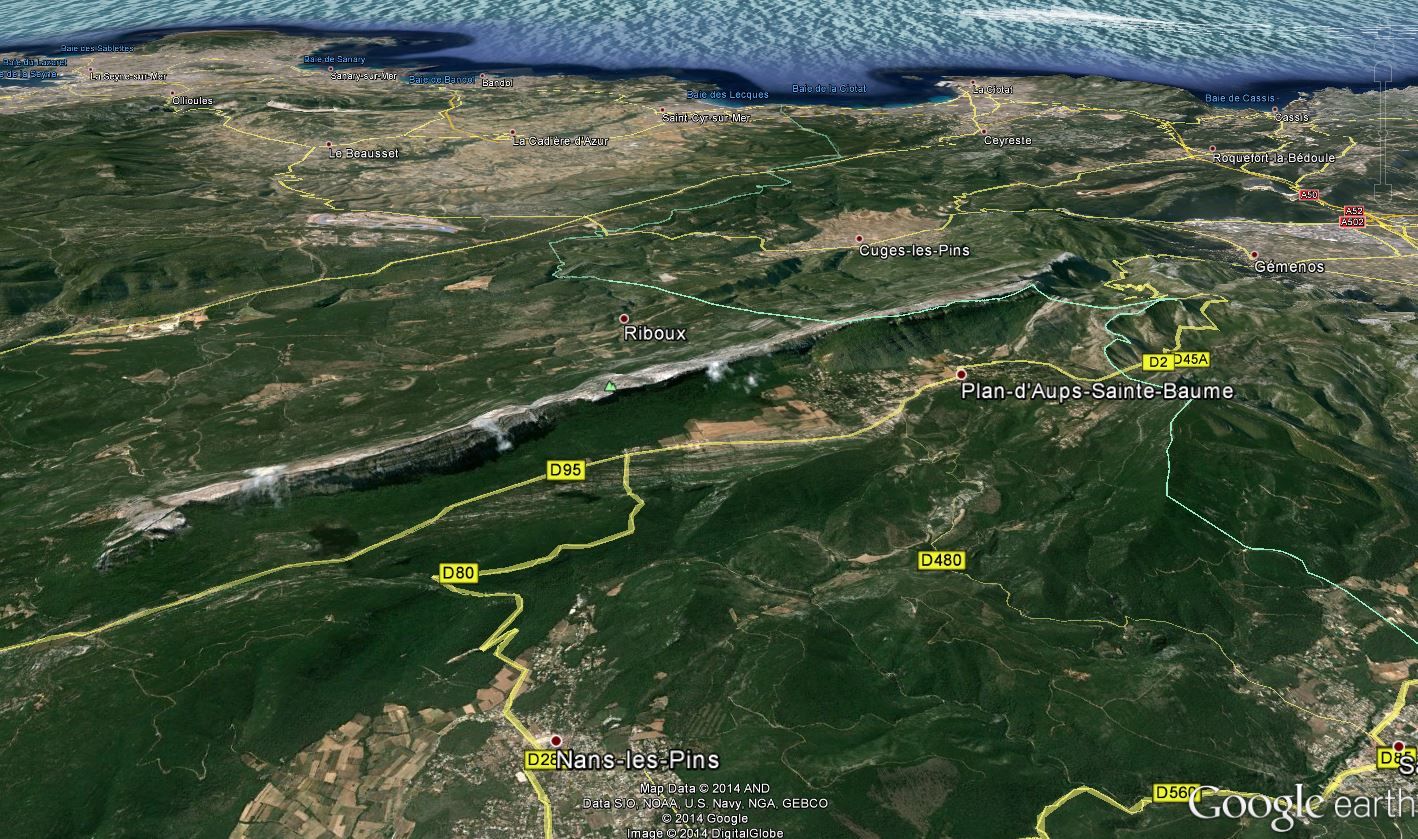
En été il fait très chaud dans cet arrière-pays balayé par un vent chaud et sec. Mais le soleil est alors beaucoup trop haut au dessus de l’horizon pour vous donner de l’ombre. Si vous faites de la marche à pied sur son versant nord, ou que vous roulez à vélo sur la D95, vous penserez inévitablement que l’automne venu, l’ombre de la Sainte-Baume sera projetée suffisamment loin pour vous donner un répit, au moins lorsque la D95 côtoie la montagne suffisamment près. En particulier, vous pourriez vous demander si, au solstice d’hiver, alors que le soleil sera au plus bas au dessus de l’horizon, une voiture garée au bord de la D95 sera dans l’ombre toute la journée, ou pas. Les cyclistes pourront avoir une interrogation similaire en ce qui concerne la route : est-ce qu’il y aura une heure de la journée où le soleil, bien que bas, sera suffisamment haut dans le ciel pour sécher la route de sa rosée nocturne ? Si comme moi, gros nerd que je suis, ce sujet vous intéresse, eh bien continuez la lecture !
Enoncé du problème

Grâce à ces clichés fournis par Google Earth, on peut évaluer la distance horizontale entre le sommet de la montagne et la D95. Etant donnée l’échelle, cette distance vaut 750 m.
La distance [B D95] vaut 750 m.
A partir de maintenant, j’appelerai“la D95” le segment de la D95 qui traverse cette longitude-là, et non pas l’ensemble de cette route.
Je sais pas pour vous, mais moi j’ai trois questions qui me viennent à mon esprit bouillonnant :
- à quelle distance horizontale l’ombre est-elle projetée quand le soleil est au plus bas dans l’année mais qu’il est à son midi (= à son point culminant dans le ciel) ?
- est-ce que la D95 est dans l’ombre de la Sainte Baume toute la journée ce jour-là ?
- Si oui, à quelle date la D95 rentre t-elle dans“le noir”, et à quelle date en sort-elle ?
On se place au solstice d’hiver, c’est la deuxième hypothèse de notre problème.
Bon, on va pas se retaper tout le calcul que je vous présente déjà dans l’article Comment calculer la hauteur du soleil à l’instant t, mais si l’on est toujours d’accord avec les approximations ci-dessous, on va piquer à cet article une équation qui nous donnera la hauteur du soleil à son point culminant pour n’importe quel jour de l’année. C’est pratique, car à partir de cet angle, on pourra calculer la distance horizontale à laquelle l’ombre du sommet de la montagne est projetée sur le terrain. Cette ombre contiendra-t-elle la D95 ? Ou bien elle ne l’atteindra-t-elle pas ?
Approximations choisies
Comme je disais dans l’article évoqué ci-dessus, comme toujours dans la nature, les choses ne sont pas des figures parfaites, alors pour utiliser l’équation démontrée dans l’autre sujet, nous allons faire les approximations suivantes :
- l’orbite de la terre autour du soleil est considérée comme circulaire.
- la vitesse orbitale de la terre est considérée comme constante sur l’année, de telle manière que son angle polaire soit proportionnel au quantième du jour.
- la terre est considérée comme sphérique, de rayon R.
- l’origine des coordonnées polaires de la terre sur son orbite, représentée par θ=0, sera arbitrairement fixée au solstice d’hiver boréal, c’est à dire le 20, 21 ou 22 décembre selon l’année.

θ = h(t) = 90° - |λP| + tan-1(tan -ε . cos(Q(t) - Q0)/365*360)Avec λP = la latitude du point D, ε l’angle d’inclinaison de la terre sur son écliptique, soit 23°26’15", Q(t) - Q0 le nombre de jours entre la date qui nous intéresse, et le solstice d’hiver. Oh ! Ca tombe bien, Q(t) = Q0, puisqu’on se place au jour où le soleil est le plus bas dans le ciel, et par définition ce jour, c’est le solstice d’hiver. Donc on connaît directement l’angle que fait le soleil avec l’horizon, puisque c’est un cas aux limites de cette équation.
Trop pratique cette équation ! Elle nous apporte directement l’expression de la hauteur du soleil, à son point culminant, en fonction du jour de l’année.
Valeur numérique de θ au solstice d’hiver :
θ0 = 90° - 43°20’30" + -23°26’15" = 46°39’30" - 23°26’30" = 23°13’00"Comme on connaît par ailleurs la hauteur de la crête de la montagne : c’est son altitude moins l’altitude de la D95, on va, grâce à la relation tangente du triangle rectangle BSD, déterminer la longueur de la base [BD].
Calcul de [BD] :

[BD] = [BS] / tan θor
[BS] = alt(S) - alt(D95) = 1103 m - 713 m = 390 md’où
[BD] = 390 / tan(23°13’) = 909 m
Réponse à la question 1 de l’énoncé du problème
L’ombre de la Sainte Baume, au solstice d’hiver, et à la longitude entendue dans notre problème, 5°47’20.48", est projetée à 909 m de la verticale de la crête.Réponse à la question 2 de l’énoncé du problème
Etant donné que la D95, à cette longitude-là, n’est qu’à 750 m de distance de la crête, alors elle est plongée dans l’ombre au midi du soleil le jour du solstice d’hiver.Réponse à la question 3 de l’énoncé du problème
Il existe bien une date d’entrée t1dans l’ombre et une date de sortie t2 de l’ombre, puisqu’au solstice d’hiver il y a 909-750 = 159 m d’ombre au nord de la D95. Mais quelles valent-elles, ces dates ?
Il faut prendre le problème à l’envers : quelle est la valeur de la hauteur du soleil θlimite = h(t1) = h(t2) qui donnerait une ombre [BD] d’exactement 750 m de longueur ? Il doit y avoir deux dates pour lesquelles on obtient ce résultat à partir de la fameuse Loi n°3.
[BD] = 750 m <=> 390 / tan(θlimite) = 750 m, soit θlimite = tan-1(390/750) = 27°28’28"Or
θlimite = 90° - 43°20’30" + tan-1(tan(-23°26’15") . cos( (Q(t) - Q0)/365*360 ))d’où l’on déduit
Q(t) - Q0/365*360 = cos-1( tan(90-θlimite-43°20’30") / tan(23°26’15"))D’où l’on déduit
|(Q(t) - Q0)/365*360| = 36 joursSoit
|(Q(t) - Q0)| = 36.5 joursC’est à dire que la date d’entrée de la D95 dans l’ombre de la Sainte Baume, au midi du soleil, se situe 36 jours avant la date du solstice d’hiver, et la date de sortie se situe symétriquement à 36 jours après. Si l’on considère un solstice d’hiver au 21 décembre, on obtient :
A cette longitude, la D95 rentre dans l’ombre à t1 = 15 novembre, et en ressort à t2 = 26 janvier.
Attention, j’insiste : je ne m’intéresse qu’au midi du soleil, au moment où il est plein sud. Car en pratique, ce morceau de D95 reçoit en fait le soleil d’hiver autour de 14h30, quand celui-ci fait un angle SSW, et que la crête qui le cachait passe sous les 1000 m d’altitude…



